The g Loop: How Intelligence Learns, Adapts and Decides - Part 1
How Your Mind Updates Its Beliefs, Adapts to Surprises, and Navigates an Increasingly Chaotic World
For the past few years, I’ve been developing a computational model of general intelligence - one that captures the computational core of IQ - of how we learn, adapt, problem solve and make decisions in an uncertain world. At the heart of this model lies the g loop, a fundamental mechanism that governs how we update our beliefs, shift between exploration and exploitation, and refine our internal maps of reality. This framework isn’t just an abstract theory - it resonates with key developments in both AI and cognitive neuroscience, offering insights into everything from machine learning algorithms to human expertise. This article provides a first window into these ideas, breaking down the mechanics of the g loop and how it explains some of the most powerful learning processes in the brain.

Introduction
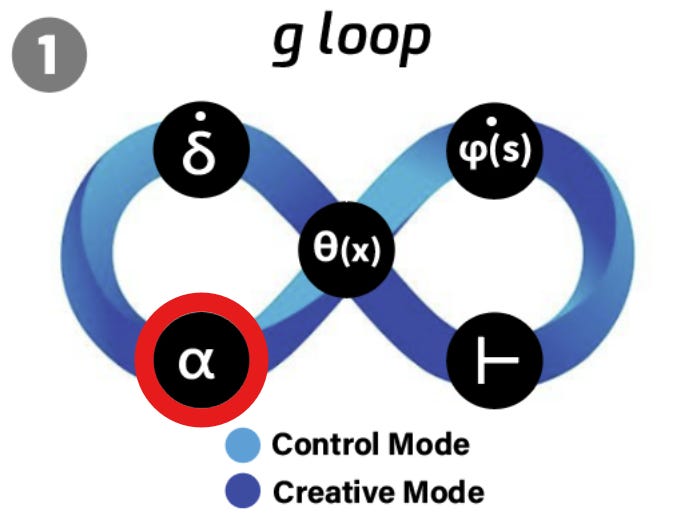
On the left, you’ll see an infinity (∞) shape labelled the g loop - our brain’s constant dance between updating what we know (via prediction errors, δ) and deciding whether to play it safe or venture into the unknown. On the right, you’ll see how we move from an initial state So to a goal state S*, all while balancing fluid intelligence (Gf) with crystallised intelligence (Gc). The g loop might be the hidden code behind how we can learn so quickly, adapt so smoothly and master just about any skill - behind our IQ.
The g loop distills foundational concepts from AI and cognitive neuroscience into one tight package, capturing the mechanics of how intelligence refines itself over time. From Bayesian reasoning to reinforcement learning principles, it resonates with the very algorithms that drive modern artificial intelligence - only our brains have been running the program for millions of years. But what does that actually mean in everyday terms?
You can think of it like this: your brain is constantly running little ‘experiments’ on reality. It makes predictions, checks how close they are to the real outcome, and then tweaks its internal model if something is off. These tweaks aren’t always the same size. Sometimes the brain goes “Woah, that was way off!” and learns super quickly. Other times it thinks, “That’s about right,” or “I need to see that again,” and barely updates at all. That’s where dynamic learning rates come in.
α governs how strongly new information reshapes our understanding.
It adjusts based on prediction error (δ) and environmental volatility (τ).
A high α means rapid learning and adaptation (when surprises are large and reliable).
A low α means stability and reliance on existing knowledge (when surprises are small or unreliable).
So, α is the star of the show in Part 1 of this introduction to the g loop, as it determines when we update our beliefs and when we stick with what we know.
It’s a bit technical - as we’re now in the territory of computational neuroscience and AI. But we’ll keep it grounded in examples - from everyday decisions like planning your next meal. So keep scrolling, because understanding this g loop might help you rethink how you learn, strategise and navigate the world. 2.
In the model diagram, you’ll notice the g loop labeled with three key elements - δ, α, and θ - plus a ϕ(s) for the internal cognitive map or ‘mental model’ we work with in any cognitive task or challenge. Keeping the math to a minimum, the main point is that each of these components helps your brain decide when to update our mental models and when to stay firm with them.
What Is the g Loop?
Think of the g loop as a self‐correcting system that’s always on guard for mismatches between what you expect and what actually happens. Each time you’re surprised by something - a bigger (or likely smaller!) bonus than you anticipated, or a bizarrely different taste in your morning coffee - your brain registers a prediction error (δ) - a standard concept in machine learning and AI. This can sometimes jolt us out of being on autopilot. The loop then uses that error signal to tweak your internal model of the world (ϕ(s)), so that next time, you (hopefully) won’t be caught off guard.
There are two types of prediction error:
Reward Surprises
We’re talking about motivational surprises here - like when you get a higher paycheck than usual (a “positive” surprise) or no paycheck at all (a “negative” surprise). These events carry emotional weight because they tell you something about your success or failure in achieving goals.Sensory Mismatches
This covers the “wait, that’s not what I expected to see/hear/feel” kind of surprise. If you reach for your coffee mug and it’s a lot lighter than usual, your brain goes “Huh?” and updates its sensory expectations accordingly.Together, these reward and sensory surprises feed into one master signal (δ) that flags how “off” your predictions were. The g loop is then all about using δ to keep your internal model ϕ(s) on track.
Key Components
Prediction Error (δ)
This is the difference between what you thought would happen and what actually happened. A large δ - like realizing the coffee mug is nearly empty when you expected it to be full - signals a significant mismatch between expectation and reality. Small δ means you were mostly correct and no update may be needed.Dynamic Learning Rate (α)
Once δ sounds the alarm, α determines how dramatically to respond. When α is high, your brain scrambles to rewire and adapt quickly - engaging fluid intelligence (Gf) to actively figure things out and revise predictions. When α is low, the system treats the mismatch as noise, allowing crystallised intelligence (Gc) - the collection of prior mental models we live by - to persist. (As an aside, Gf is more energetically costly - and more likely to be experienced as stress - than Gc as a rule.)Decision Threshold (θ)
Finally, θ acts as your brain’s internal gatekeeper, deciding whether to explore new strategies (Gf) or stick with known ones (Gc). If recent surprises (δ) have been big and reliable, θ lowers, inviting exploration and a shift toward fluid reasoning. If not, θ remains high, keeping cognitive effort minimal and relying on autopilot strategies and our existing mental models ϕ(s).
Put simply, the g loop is the system that takes your daily dose of surprises - good, bad, or weird - and uses them to refine how you see and act in the world. The spilled coffee incident is a trivial but insightful example: a single surprise (δ) might not override an established habit (Gc), but a repeated pattern of unexpected outcomes could lower θ, increasing reliance on adaptive learning (Gf).
Next, we’ll zoom in on that second component, the dynamic learning rate (α), to see why it’s so crucial for everything from your best decision-making moments to those times you finally nail a tricky new skill.
The Core Concept: Dynamic Learning Rate (α)
So far, we’ve talked about how the g loop is constantly tweaking your internal model of the world by tracking prediction errors (δ). But here’s the real magic trick: not every surprise triggers the same level of learning.
Your brain doesn’t just blindly update everything all at once - that would be chaos. Instead, it has a built-in ‘volume knob’ for learning, adjusting how much weight to give new information. That’s α, the dynamic learning rate.
Sometimes, α cranks up to max - when the world blindsides you with something you never saw coming. Other times, it dials way down, letting you rely on what you already know.
Computational Basis in Everyday Language
Let’s break this down with an everyday example.
Imagine you’re trying out a new coffee shop. You take your first sip and - wow - it’s way stronger than expected. That’s a big prediction error (δ), meaning your internal model (“this is what coffee should taste like”) just took a hit.
What happens next? If this is your first visit to the café, your learning rate (α) will be high - you’ll quickly update your expectations: Okay, this place serves stronger coffee than I’m used to. But if you’ve already been here ten times and this is just a one-off variation, your α stays low. Your brain chalks it up as a fluke, and your coffee expectations remain mostly unchanged.
In other words, α helps you weigh new experiences against past knowledge. Generally, the more uncertain or surprising the world is, the more you learn. The more stable and predictable things are - over meaningful time scales - the more you stick with what you know.
Formula Simplified: How α Adapts
While the math behind α can get technical, here’s the intuition behind it:
α increases when:
You’ve just experienced a big prediction error (δ) - something turned out very differently than expected.
The environment is volatile - things are changing rapidly, so you need to keep up. Like the current political environment!
α decreases when:
Errors are small - you’re mostly getting things right, so no need for major updates.
The environment is stable - if things have been consistent, it’s better to trust what you already know.
A rough way to think about this is:
Where:
|δ_recent| = the size of recent surprises
τ (tau) = how unpredictable the environment is
This means big surprises in a chaotic world make you learn faster, while small surprises in a stable world make you stick to your existing knowledge.
I would say we increasingly live in a world where we need the former - big α !
Why This Matters for Learning and Decision-Making
This dynamic learning rate is what keeps your brain agile yet stable. It lets you shift between exploring new ideas when needed and exploiting what you already know when things are predictable.
It’s why you learn a new language faster when you first start, but it slows down once you get the basics.
It’s why first impressions matter so much - early surprises have a bigger impact on updating your expectations.
And it’s why experienced decision-makers don’t overreact to minor surprises or anomalies - they’ve seen it all before, so their α stays low unless something truly different happens.
Now that we’ve got a handle on how α works, let’s take things a step further: how does this principle shape strategic thinking in decision-making and skill learning? Stay tuned - we’re about to dive into Bayesian reasoning - one of the key thinking strategies in IQMindware’s strategic IQ module.
Dynamic Learning Rate in Bayesian Reasoning and Decision Making
So now that we know α (the dynamic learning rate) is your brain’s ‘volume knob’ for updating beliefs, let’s talk about one of the most powerful ways this plays out in everyday thinking: Bayesian reasoning.
Bayesian reasoning is fundamental in machine learning, AI and neuroscience.
If you’ve ever changed your mind based on new evidence, you were (perhaps unknowingly) thinking like a Bayesian. Bayesian reasoning is all about continuously updating your beliefs as fresh information comes in - but, just like we saw with α, not all new data gets equal weight.
Let’s break it down.
Bayesian Reasoning: The Basics
Imagine you’re playing poker and a new player sits at the table. You have no idea if they’re a pro or a total noob (newbie). So, you start with a neutral assumption: They could be either.
The first hand, they make a bold bluff and win. Huh.
The second hand, they pull off another smart move.
By the third hand, you’re thinking: Okay, this person might actually be a pro.
That’s Bayesian reasoning in action. With each new piece of evidence, you’re updating your prior beliefs based on the likelihood that what you just saw matches a given hypothesis (e.g., “They’re an experienced player”).
At first, big surprises carry more weight - your learning rate (α) is high because you have no strong prior beliefs. But as the game goes on, your updates slow down - you’re no longer as surprised, so α drops, stabilising your belief - your ‘mental model’.
In short: When uncertainty is high, you adjust quickly. When confidence is high, you adjust slowly.
How the g Loop Ties In
Bayesian updating and the g loop go hand in hand. Remember how prediction error (δ) tells your brain when something unexpected happens, and α (dynamic learning rate) controls how fast you adapt?
Here’s the connection:
Big, reliable prediction errors (δ) → High α → Fast Bayesian updates. Engage fluid intelligence (Gf).
Small or noisy prediction errors → Low α → Slow Bayesian updates (stick with what you know - with crystallised intelligence (Gc)).
This means your brain is constantly weighing the reliability of new evidence before deciding how much to learn from it.
Example: Imagine you hear a rumour that your favourite coffee shop is closing.
If multiple sources confirm it, your prediction error (δ) stays high, α remains elevated, and you quickly accept it as fact.
If it’s just one vague comment, α stays low, and you wait for more evidence before believing it.
This built-in skepticism prevents you from overreacting to unreliable information while still allowing for rapid updates when the evidence is strong.
Bayesian Reasoning in Everyday Decisions
Now, let’s put this into real-world situations where Bayesian updating + the g loop = smarter decisions.
1. Planning a Picnic (Dealing with Uncertainty)
You check the weather forecast in the morning - it says 10% chance of rain. Looks good! You confidently plan a picnic.
But at noon, dark clouds start rolling in. Uh-oh. That’s a big sensory prediction error (δ) - your expectations (sunny skies) don’t match the new evidence (gloomy clouds).
At this point, your learning rate (α) jumps up, and you quickly revise your belief: Maybe the forecast was wrong. You check again - it now says 50% chance of rain. At this point, you grab an umbrella and start looking for an indoor backup plan.
Bayesian update complete. The bigger the surprise, the faster you learn.
2. Investing (Avoiding Overreaction)
Imagine you’re investing in Bitcoin. One day, the Bitcoin price drops 5%.
A noob investor might panic (“Sell!”), treating this small dip as a huge prediction error (δ). But a seasoned investor - who has seen countless market fluctuations over the months - has a low α for this kind of noise. They stick with their prior belief that markets naturally fluctuate and don’t overreact.
But if multiple unexpected factors (reports, legal trouble, etc.) start piling up, their α will increase - indicating it’s time to update their strategy.
The key here? Knowing when to adapt and when to stay the course.
Strategic Thinking Impact: Smarter, Faster, More Adaptive
By fine-tuning how much we trust new information, the g loop makes Bayesian reasoning second nature.
In high-uncertainty situations (new job, new skill, new opponent), α stays high, and you learn quickly.
In stable, familiar environments (daily routine, long-held beliefs), α stays low, so you don’t constantly second-guess yourself.
This adaptability is what makes human intelligence so powerful. The best decision-makers - whether in business, science, or even poker - are the ones who know how to adjust their learning rate at the right time.
Next Up: Recursive Skill Learning
Now that we’ve seen how the g loop helps us adapt our beliefs, what about learning skills? How does your brain decide when to explore new techniques versus when to lock in what you already know?
That’s where recursive skill learning comes in. If you’ve ever gone from clumsy beginner to smooth expert - whether in chess, coding, or cooking - you’ve experienced this process firsthand.
In the next article, I’ll use the wonderful g loop to break down why prediction errors drive skill mastery, how your learning rate shifts as you improve, and why failing fast is the secret to getting good.
Stay tuned…